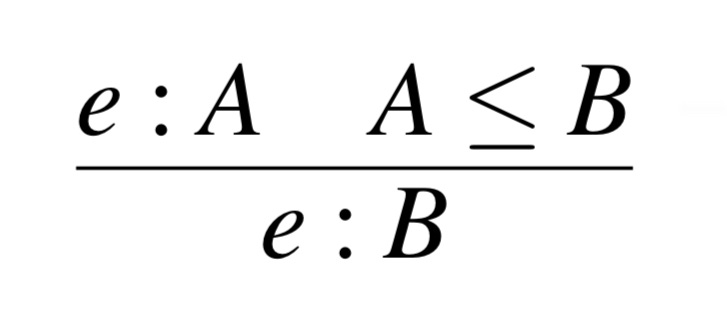A Home for Intuitionistic Type Theory in Conceptual Engineering
Through the thick philosophical forest, comes a somewhat useful tool for a somewhat useful brain.
Read This Preamble Please :)
I wrote the following “essay” as my final paper for my Metaphysics class on Conceptual Engineering. There is a lot of background and context that will be missing from the reading itself, and I am too lazy to add it for this blogpost. Nonetheless, I really liked the topic and the esoteric nature of applying philosophical tools to the least expected areas, in this case math.
I don’t expect this to be an easy read, because of the technical background and my poor writing skills. Still, I hope the average reader can get something out of this, ideally what conceptual engineering is useful for.
Throughout the text I reference Tanswell’s 2018 paper, and it’s because it’s the paper which my entire text is based on! I suggest giving that a read before mine as it will give a more in-depth insight as to what I’m rambling about. Anyways, I’ll stop distracting your precious reading time, enjoy.
Abstract
Recent discussion in the application of conceptual engineering in mathematics has attempted to engineer fundamental disagreements in regard to the foundation of mathematics, namely, ZFC set theory. However, such discussions ignore and implicitly appeal to various schools of thought in the philosophy of mathematics to apply conceptual engineering techniques. This has resulted in an obscure and contradictory way forward to engineer such disagreements. This paper seeks to frame the discussion of conceptually engineering mathematical concepts in the intuitionistic school of mathematical thought, providing a clearer foundation for the conceptual nature of mathematics. Intuitionistic type theory is an extension of type theory that embeds typed first-order logic and a form of structural type theory. ITT focuses on the practical foundations of mathematics, and as a result, emphasizes conceptual natural formalizations that concentrate the essence of practice. From a practical foundations point of view, the idea of conceptually engineering mathematics should become clearer as we follow a series of natural deductions rather than axiomatic systems from the formalist school of thought. This analysis gives way to further understanding of what we ought to use intuitionistic type theory for; consequentially what the practical foundation of mathematics should accomplish. We perform a case study by conceptually engineering coercion–“what does it mean for a term to have more than one type”–and type-theoretic applications that follow. We finally provide a general framework for identifying concepts in higher-order mathematics that require conceptual engineering, and present a computational approach for reducing such concepts to their ITT analog for engineering in a deterministic domain.
Introduction
Conceptual engineering undertakes an ameliorative process behind the design and evaluation of our concepts (Isaac, Koch, and Nefdt 2022). It is believed that our conceptual ability can be re-engineered for the better, resulting in an adequate set of concepts which ought to accomplish a certain goal. This normative approach is reliant on whatever modality (environment) we are operating in—i.e., engineering the social concept of woman is significantly dependent on the inequalities of a particular social environment, whereas engineering the scientific concept of oxygen depends on preliminary work in an objective descriptive environment. Either way, both concepts are still closed under conceptual engineering because we are attempting to ameliorate this bridge between our cognitive interpretation of such devices and their functional efficacy. Isaac, Koch, and Nefdt 2022 propose a methodology for improving specific ameliorations: tackling natural language semantics for rich languages. This framework follows naturally for linguistic misconceptions—i.e., verbal disputes (Chalmers 2011). The descriptive nature of a given concept ought to be founded in a common reference point for all utterances of any given rational party.
Work in the conceptual engineering of mathematics by Tanswell 2018 has provided non-trivial evidence towards the fact that mathematicians are sorts of conceptual engineers, in particular the analysis of mathematics not classified as a conceptual safe space. However, further analysis of Tanswell’s methodology towards conceptually engineering mathematics is obfuscated due to a lack of a concrete modality/environment. The same follows for social concepts, such as the woman example: we have to set the stage for a social context for the inequalities towards the concept of woman we seek to engineer. Mathematics also has to be framed within an environment in which it makes sense to engineer, whether or not that foundation believes in an underlying truth for mathematics is non-trivial. Tanswell 2018, unapologetically, glosses over whether the central point of the analysis is about our use of language and not the mathematical concepts per se. If the former, the analysis would naturally follow a linguistic analysis as previously mentioned. A lack of environment then leads to vague conclusions. To remedy the ambiguities underlying the methodology of conceptually engineering mathematics, we propose framing the conversation under a certain school of thought which lends itself to a naturalistic approach rather than a descriptive preamble: intuitionism.
It seems tempting to take mathematics in parallel to scientific concepts which have been engineered, such as phlogiston to oxygen. The key issue with the previously stated methodology is that we are translating the concept based on its descriptor “what we have been doing all along without realizing it” (Isaac 2021), and as we gain more descriptive knowledge, we can assert a translation between an antiquated concept and it’s up-to-date version. For mathematics, we would have to strongly assert that there is an undiscovered truth to mathematics we should engineer. Tanswell 2018 discusses a plausible candidate for such a truth as the Multiverse versus Universe dilemma in set theory, what Tanswell takes to be the most foundational reduction of mathematics. Such a view would correlate with the formalist school of thought; there are no mental constructions in mathematics, just a set of symbols which are embodied by concrete objects, and mathematics is no more than a formal game of interpreting uninterpreted strings of symbols. Such a framework would essentially violate the manifest/operative methodology for identifying what is the essential nature of mathematics (manifest) and how mathematics is actively applied (operative). Using Haslanger 2005’s analysis, a formalist would not agree this be the case for mathematics in particular, given it is made up of logical axioms rather than naturalistic derivation: “Yet we should keep in mind that ‘our’ concept may not be univocal; in our haste to find a univocal concept we may obscure how the concept works in a complex social context.” (Root 2013)
Tanswell argues that this comment reinforces the idea that the general population, in this case, mathematicians, do not have to be in complete agreement. While this analysis works for the domain-specific problem within set theory, the author themselves argue that this could not be the only possible foundation for mathematics. In a greater context, it seems that following the formal school of thought, we would reach a wall made out of bedrock in which we have exhausted all descriptions for mathematics and it would be valid to refer to mathematics as a safe space. However interesting it may be to take this approach – of treating mathematics as having an underlying unfound fundamental truth – manifest/operative methodology falls short to when attempting to identify without serious technical work. Simply due to the fact that there is so much uncertainty in the foundations of mathematics, to begin with, we seem to have a clear grasp on all operative concepts for mathematics, albeit that is all we know. Proposals for manifest concepts are too limited; Tanswell 2018 references this problem in the selection of the current most studied foundation possible, ZFC, when operated to topology.
“ However, even if we were to find those who did happen to know how to translate the main concepts into set theory, de Toffoli & Giardino demonstrate that the kind of operations licensed by the topological concepts are often visual, diagrammatic and manipulative (in a tactile sense)— far removed from those which one would find in the setting of set theory. So the operative concepts, i.e. the concepts as employed in practice, are frequently not set-theoretical.” (Tanswell 2018)
Afterward the author notes an objection to the fact that there is not a single foundation available, instead a whole array of foundational theories that ease translations in mathematics. This approach is therefore better expanded on through the intuitionist lens rather than the formalist. We can declare that there exists a constructed – therefore infinite (Brouwer 2011) – the number of foundations for mathematics, rather that we have to technically struggle to find all the foundations of mathematics.
Intuitionists deal with mathematics constructively, naturally giving way to Haslanger’s methodology. Rather than using a descriptive analysis approach for the conceptual engineering of mathematics, the tools lend themselves elegantly to the social construction of concepts! Therefore, this paper will continue with an assumption of mathematical construction. In Brouwer 2011, Brouwer describes the belief in the universal validity of the law of excluded middle as a phenomenon of the history of civilization, similar to the belief of the rationality of π. An intuitionistic framework fits perfectly under Haslanger’s manifest/operative analysis, further clarifying what we ought to conceptually do with mathematics1:
“The intuitionist tries to explain the long duration of the reign of this dogma by two facts: firstly that within an arbitrarily given domain of mathematical entities, the noncontradictory of the principle for a single assertion is easily recognized; secondly that in studying an extensive group of simple every-day phenomena of the exterior world, careful application of the whole of classical logic was never found to lead to error.” (Brouwer 2011)
Such a framework is still missing a tool to concretely conceptually engineer, we cannot just engineer abstract concepts with no concrete representation—even the formalists concretely map the set of symbols to a real-world application of natural numbers (counting sticks for example)! Tanswell proposes the use of Zermelo’s Axiomatization of Set Theory (ZFC) as the foundational tool for reducing mathematics. However, as Tanswell acknowledges, there are other alternatives that offer a more sophisticated or modern approach. Thankfully, Brouwer’s intuitionistic framework has been embedded within a convenient tool for such analysis: Per Martin-Lof’s type theory, also known as intuitionistic type theory (ITT). The choice of ITT is also motivated by the nature of type theory compared to set theory. This decision is not to say that type theory is more general than set theory, nor more foundational (other domains such as Category Theory will not be discussed, although it serves as an alternative for generalizations).
In type theory, the focus shifts from the possible objects in a set (ZFC), and instead, we study the objects of the possible operation in a set. Each element is reserved to have a type, and a set of typing rules (those which follow the style of inference rules in first-order logic), describe their relations. For example, objects with type o : N can only operate on other objects with the same type N, i.e., we can only add naturals with other naturals when counting. This behavior is more interesting to study in the context of conceptual engineering; type theory is concerned with the practical foundations of mathematics whereas set theory is concerned with the proof-theoretic foundations of formal systems. Practical foundations are better suited for Haslanger’s manifest/operative duality, as we emphasize a conceptual natural formalization based on the essence of practice.2
In Section 2, we discuss in more detail the benefits of using intuitionism as the mathematical framework for conceptual engineering and the most cited recount of practical foundations. In this recounting, we will discuss Haslanger’s manifest/operative methodology and frame it in the context of mathematics at a broad scale, using the theorems from practical foundations as a guideline for which concepts are manifest and which are operative. Following, in Section 3, we will outline Tanswell’s use of Waismann’s notion of open texture and define clear analogs to ITT. Arguments towards the open-texturedness of mathematics follow those enumerated by Tanswell 2018. Section 4 will discuss ambiguities in modern-day ITT and foundational roadblocks which have concrete consequences in practical mathematically-driven work, i.e., the development of homotopy-type theory. Section 5 will present a case-study for conceptual engineering concepts in ITT, particularly the concept of coercion. Finally, Section 6 will generalize this process for conceptually engineering any concept from ITT, outlining a general ruleset for identifying concepts that require conceptually engineering in higher-order mathematics, and how to find their ITT reduction (such is done through the lense of modern computational techniques.)
Framework
Conceptual engineering as a school of thought in mathematics.
The term practical foundations of mathematics was introduced by Taylor 1999 to introduce a foundational framework for theories in mathematics based on natural transformations. Before, the term ”foundations of mathematics” was used to refer exclusively to the unknown building blocks of pure mathematics, all in an attempt to solve problems in this domain. Taylor 1999 came from a background concentrated on the essence of practice and how to guide the practice of mathematics in a more applied world. This is particularly evident in Taylor’s categorization of the foundations of algebraic topology and the mechanical foundations of elasticity and fluid mechanics (Lawvere 2003). These systems are natural deductions: type-theoretic deductions that help natural expressions represent central concepts in mathematics.
We don’t have a technical need to get into the details of the construction of natural deductions for this analysis. At high-level natural deductions describes a deductive system that simulates natural deductive reasoning, i.e., we reason from assumptions rather than axiomatic proofs. This is done through two rules, introduction and elimination. The introduction allows us to come to natural conclusions given a set of judgments, whereas elimination allows us to come to natural conclusions from an already built judgment (one that has been already introduced). For example, the conjunctive operator ∧ can be introduced from the following propositions: (1) Allice owes Bob, (2) Bob owes Cameron, therefore (3) (Allice owes Bob) ∧ (Bob owes Cameron). The elimination of (3) produces both (1) and (2). When the rules don’t contradict each other, this is referred to as harmony. A disharmonious deduction would be: given (3), Bob owes Allice.
These natural deductions follow deductive reasoning as expected. In this framework, we shall discuss all mathematical truths as a process of reasoning passing from discovered premises to conclusions such that the truth of the former necessitates the truth of the latter. This view does change our application of open texture, which will be discussed in Section 3, but for now, we can continue with the usefulness of this approach in conceptual engineering. It follows under this framework that we can build deductions top-down rather than axiomatically, hence a practical foundation (in this context). For conceptual engineering, we now have a concrete – operative – a set of premises we deal with on a daily basis, outside and inside of mathematical maturity. We can then, from these premises, introduce and eliminate a foundational manifest to engineer such concepts. This function has the shape of a surjective mapping: there will always be a foundational concept to map to, and concepts will have, although not necessarily, the same foundation. This is similar to bedrock concepts introduced by Chalmers 2011, however, the key distinction is that we will be using the mappings as the concept to engineer, although it still keeps track of the range of our mathematical concepts. This mapping isn’t to say that these are the foundational theories for each concept, rather it gives us a sense of the domain each concept belongs to, for example, topological problems will live in a diagrammatic domain.
We keep track of these domains through the application of natural deductions in type theory, in particular, ITT. The premises are loaded with a type. For example, following the conjunctive definition, in type theory,, we would use a cartesian produce instead. Two terms a,b belong to corresponding types A, B to form the judgment a : A, b : B. This is just to say, that given the pair (a, b) we know it must be of type A × B; this is the introduction rule. The elimination rule would follow similarly, given the premise of type A × B, we can conclude that there is a term in the premise p of type A and another of type B. In type theory, we care about the rules for what objects can do, rather than the objects themselves. Natural deduction in this case frames the domains for an arbitrarily complex set of terms with a given type. Topologically-loaded terms will have diagrammatic types, which exhibit natural rules3 that clearly deduces to a diagrammatic manifest (discussion of this manifest/operative concept we put forward is discussed in more detail in Section 2.3).
The last important rule to note for ITT is hypothetical reasoning. Hypothetical reasoning allows us to reason from assumptions given hypothetical judgments. This lets us make hypothetical judgments B assuming type A, notated as A ⊢ B. This is more powerful than it seems, as it allows for an arbitrary amount of hypotheses in which the judgment is true. For example, the logical rule of implications =⇒ would be of the form: given an arbitrary hypothesis Γ, and A ⊢ B, then Γ ⊢ A =⇒ B. This a priori usage of hypothetical judgments facilitates the provability of theorems and is foundational to our analysis. There are more rules that exhaust questions in decidability, but these are not necessary for the rest of our discussion. Since this framework has loaded practical foundations, a top-down approach, I will be referring to this particular use of terminology as the ITT-CE framework.
Practial versus Proof-theoretic foundations of mathematics.
Tanswell 2018 seems to take an approach with proof-theoretic foundations instead. These focus on making use of a particular and arbitrarily complex set of formal systems to prove foundational theorems. Tanswell discusses the archetypical system ZFC set theory for such analysis. Rather than type theory, this framework makes use of proof theory, the study is of formal proofs. Since Go ̈del’s incompleteness theorem, approaches within proof theory making use of natural deduction have been developed (Negri and Plato 2008). However, as previously mentioned in Section 1, it isn’t clear how to introduce seemingly contradictory domains within the manifest/operative concept for a particular system, such as ZFC. This limits the types of natural deduction, which consequentially limits the number of mathematical concepts to engineer drastically. Although selectively constructive approaches in proof theory do exist, their complexity and monomorphic nature obscure the conversation when conceptually engineering.4
Manifest/operative concepts on practical foundations.
Haslanger 2005 produces an ameliorative project for constructing new concepts in social justice: the manifest/operative concept. There are three concepts in this methodology: manifest, operative, and target concepts. The manifest concept refers to what we take ourselves doing in a given scenario, the operative is what we actually are doing in practice, and the target is what we should ideally be doing. Tanswell does not discuss target concepts in the mathematical analysis, which I do not agree with and will be discussing in Section 4. The reasoning following this methodology is similar, it reinforces the idea that mathematics is not a safe space and demonstrates an applicable use of conceptual engineering in mathematics. Tanswell uses definitions in axiomatic systems, namely ZFC, as the manifest concept, whereas the operative concepts are what we learn in mathematics education, essentially mathematics without maturity. Although Tanswell 2018 provides various quotes from experts advocating for manifest concepts making use of set theory, we’ve established such a view is too narrow. Therefore, even though this might not reasonably represent the real world view of most mathematicians, our manifest concept is defined by those in the intuitionist school.
Esik 2006, Lambek and Scott 1986, Harper 2011, Eades 2012, and Goguen 1991 are a few authors which take conceptual trinitarianism as the key towards the foundation of mathematics. The classical trilogy describes three notions of mathematics that are equivalent: intuitionistic type theory, programming language theory, and category theory/topos theory. The idea is that the three subjects are different perspectives showcasing the same idea (Lambek and Scott 1986).
“The central dogma of computational trinitarianism holds that Logic, Languages, and Categories are but three manifestations of one divine notion of computation. There is no preferred route to enlightenment: each aspect provides insights that comprise the experience of computation in our lives.” (Eades 2012)
The trinitarianism establishes that if you arrive to a conclusion in one aspect you should be able to derive meaning for the other two as well. Because of this, we can take ITT as our foundational manifest concept, although either languages or topology could be used the same.5 The operative concepts are therefore the rest of applied mathematics, i.e., the mathematical terms from which we load types. In this framework, we exhibit a strong correlation between manifest and operative concepts by having manifest concepts load information for the operative concepts, thus we always know which domain we are in. For example, we know each domain needs to have a function type for transformations from one type to another in that domain. The natural deduction for functions can easily be notated with their programming language analog (we’ve already established this is equivalent to ITT). For a given term x, λx.b is equivalent to b(x) in the language reduction. The introduction rule for this would then follow Γ,(x : A) ⊢ (b : B) then Γ ⊢ (λx.b : A → B). The operative concept is our naive conceptualization of b(x) in whatever domain we find ourselves in, the manifest concept is the translation to the programming language analog λx.b, and the target is our type information A → B. We’ll go into more information about the target concept in Section 4, but for now, it should be noted that ITT-CE is beneficial to use for this conceptual engineering analysis because all reduced information has type information we can use to classify the domain (whatever A and B be).
Open Texture & The Safe Space-State of ITT-CE
We have been taking for granted an important question hitherto: is ITT-CE a safe space? By Tanswell 2018’s description of Shapiro’s notion of Open Texture, we make use of the following:
“(Open Texture) A concept or term displays open texture iff there are cases for which a competent, rational agent may acceptably assert either that the concept applies or that it disapplies.” (Tanswell 2018)
Tanswell uses an, in our opinion, an antiquated example of heuristic counterexamples brought by Lakatos’ notion of a polyhedron. There is a disagreement on the defense for Euler’s theorem in regards to several polyhedra, therefore there must exist open texture by the rational freedom to choose different responses. There is a problem regarding this approach in the formalist view, which is that one could always argue that the set-theoretic notion of a polyhedron is a closed texture. Tanswell gets around this issue by asserting that “if concepts are only properly delimited for a specific domain of application, this does not point to us being in control of them in general.” This point follows for our trinitarianism as well. It follows for a constructivist framework that mathematics is in constant development and evolution, therefore we introduce new ideas which haven’t been previously established, and we can get rid of naivete ́ as we see fit. A constructivist’s argument is much closer to that of socially constructed concepts. For example, the term mother can be taken to be socially constructed as the baby birth-er, at least from a manifest standpoint the biological mother. There is no ground truth for motherhood, just a construction that maps from a convenient operative concept. However, if there would be a scientific advancement that allows for multiple women to carry the same baby, the term mother would necessitate change.
This notion of open texturedness is difficult to justify from the formalist school in which there exists an objective truth that is not constructed, however, we are working with ITT-CE! Following the same logic as with the motherhood example, we can take any concept from mathematics and extend it as necessary, in particular thanks to our previously described notion of hypothetical judgments. With ITT-CE, we can generalize target information (type information) in an arbitrary environment, and this construct is inherently open-textured in the constructive sense.
Thus, we can avoid the analysis on backstage and frontstage mathematics, i.e., the distinction between the context of discovery and the context of justification. This distinction asserts that mathematics is separated into the realm of intuitive informalisms and formal rigorous results, however, we take into account that all of mathematics is backstage or informal in nature, and made up of natural deductions. Even though it could be argued that mathematics under this domain is a safe space because we exhibit full control, it still is not the case that mathematics is free from the complexities of natural language itself. As Brouwer 2011 notes in his construction of intuitionism, mathematics is but a temporal operative concept (based on time as the foundational aspects of arithmetic) which is continuously constructed (because time is continuous) into manifest mappings for what we know as higher level mathematics. Mathematics is not a safe space because, similar to our language-driven constructions, it suffers from imperfect/non-exhaustive mappings.
So far, we have established ITT-CE, a framework for conceptually engineering all of mathematics, and how to identify the mathematical terms we are conceptually engineering. We have also identified ITT-CE as being open-textured and not a safe space. But we have just justified the need for conceptual engineering by arbitrary environments which would need an extension. Although this satisfies the minimum, we still don’t have a good incentive for conceptual engineering rather than just doing the technical work, much less justify ITT-CE mathematicians as sorts of conceptual engineers. What is the fundamental problem in ITT?
While there are several open problems in ITT (Open Problems in HoTT n.d.), in particular, homotopy type theory (HoTT) – a variant of ITT we’ll be using for our case study – most of the interesting work to conceptual engineer comes from the metatheory of univalence (translations from a foundational aspect of the trilogy to another, such as Homotopy theory, topos theory, to HoTT). Similar to the issues discussed by Tanswell 2018 with regards to the Universe versus Multiverse point of view, HoTT takes into consideration the univalent foundations, in which mathematical objects are built out of types. The standard problems include developing a constructive variant of the univalence axiom (to fit ITT rather and have a fully constructive system) and extending the constructive system to allow the implementation of resizing rules.6 Ideally, ITT-CE helps ameliorate confusion when developing a construction for the univalence axiom by creating a clear path for technically-skilled agents to follow.
Target concept in HoTT.
We don’t expect to exhaust a theory for constructing the univalence axiom, but we can point out the target concept for what we ought to do in HoTT. There is a defect of ambiguity, as Tanswell points out with the concept of a set when it comes to the concept of univalence. The univalence axiom asserts (A = B) ≃ (A ≃ B), that is, identity is equivalent to equivalence. It’s well known (Awodey, Pelayo, and Warren 2013) that from the homotopical view, this is a natural assumption, however, in logic it is revolutionary. The axiom establishes that isomorphic objects can be identified, whereas classically mathematicians identify isomorphic structures without official justification. This is an incredibly important discovery in logic due to the nature of programming languages and the formalization of automatic systems of identification. If we can identify equivalent definitions, we can make program and data refinement possible!7 Work towards constructing the axiom by Cohen et al. 2016 has shown serious promise. The authors provide a general framework for analyzing the uniformity condition, which applies to a specific subset of sets. However, there are still open problems recited in the understanding of the axiom, in particular a proof of canonicity. The conceptual defect here lies in what should the univalence axiom strive for, non-technically. Tanswell 2018 presents work from Mathy forthcoming which follows a survey of the various aims of set-theoretic foundations. However, we can still apply this same set of guidelines, because the survey also includes Category Theory, which is the main tool used for identifying presheaf semantics for the constructivist view of the univalence axiom, and the main tool for applying HoTT. The goals follow as such:
Metamathematical Corral To “allow for meta-mathematical consideration of the whole expanse of the vast subject at once”.
Elucidation To “provide the conceptual resources and construction techniques to clarify old mathematical notions in order to take on new demands”.
Risk Assessment To provide a scale of consistency strength (such as by using the hierarchy of large cardinals.)
Shared Standard To “serve as a benchmark of mathematical proof”.
Generous Arena To give “a framework in which the various branches of mathematics appear side-by-side so that results, methods, and resources can be pooled”. (Tanswell 2018)
Tanswell notes that the Generous Arena does not fit their manifest/operative concepts, but it does work for our analysis, such that our manifest/operative concepts work in tandem to provide target (type) information. This is our target concept. It should be clear that the target (type information) should be beneficial to identify the domain of a sequence of terms. This process allows for establishing a reductive commonality with all terms in regards to their type of information, by trinitarianism, establishing the framework required to pool from several resources. For example, if need be for diagrammatic interpretations, we can get the same type of information from the topos theory view, and translate it to a non-diagrammatic view for other use, such as computing purposes. The rest of the list is also important, but follows naturally from the higher-level constructivist viewpoints as previously mentioned, and disagrees with Tanswell’s counterexamples for Shared Standard and Metamathematical Corral in particular.
Case Study: coercion
To make this process more concrete, a simpler issue discussed commonly in ITT is the concept of coercion: What does it mean for a term to have more than one type? Such is important in the interpretation of polymorphism, where the same function is used in more than one type. The concept is also useful for type theories in philosophy, as described by Soloviev and Luo 2001. To conceptually engineer coercion, we apply the following:
Identify manifest/operative concepts: Give the ambiguous subsumption rule for coercion, we have to clarify the meaning:
Recall that ITT-CE is a top-bottom approach, therefore we start with the operative concepts. In this case, operatively we use subtyping to refer to an embedding of types, i.e., B ⊆ A := [B ,→ A] is saying that A is a supertype of B, this notion can be analogs to that of subsets. The manifest concept would then have to be represented by e, the expression that allows applying subtyping to types implicitly. This can also be simply interpreted as coercive subtyping. For example, we have that Z ⊆ R, subtyping may be coercive because R and Z are in different domains. This then changes the value it is applied to. From this information, we can get the template for our target concept A ≤ B.
Match the target concept with Maddy’s goals: This is when the technical work comes into play. It is a conceptual engineer’s job, or the prelude for a mathematician’s casework, to establish a path for the target concept. There are currently two interpretations for this subsumption rule:
inclusion interpretation: Based on types a ́ la Curry; the idea that types are properties of terms. The subsumption rule is interpreted literally, it asserts that if e satisfies the property A, and A entails B, then e satisfies B. This view however seems to not coincide with Risk Assessment, because we give meaning to untyped terms. A rational agent would have to make the choice and evaluate whether these structures are more coarse-grained given their manifest context, for example, if the expression e is in the domain of pure lambda calculus, then it is worth engineering this subsumption to this interpretation.
coercion interpretation: Based on the intrinsic a ́ la Church view; the idea that we introduce an implicit coercion from A → B. Subtyping serves as a shorthand to avoid writing the full coercion (conversion to a different data type). The issue with this interpretation follows coherence. It violates Metamathematical Corral, as it would be ideal to know that all of the results in equivalent coercions from A → B, this would be difficult if there is more than one way of deriving A ≤ B. We want the meaning of a well-typed term to be independent of its typing derivation. A rational agent would re-engineer this subsumption if there has been proven to be only one way of deriving the subtyping judgment!
A general framework towards identifying weak concepts in mathematics
As we’ve shown, the methodology for conceptually engineering concepts in ITT-CE is dependent on the domain of the problem in the context of a constructed environment. We don’t have to follow Maddy’s goals exactly, as more goals can show up depending on the context. However, the identification of weak concepts always follows situations in which a given operation has various interpretations that are valid for different edge cases. Instead of exhausting definitions for a polymorphic term, it is best for mathematicians to use conceptual engineering and apply interpretations when necessary, making use of the manifest/operative concepts to naturally deduce a target template. For example, if a problem arises in the diagrammatic interpretation of a topological theorem, a reduction in the language’s manifest can help shape the target template for a better-suited direction.
This methodology is not revolutionary nor new, it is what mathematicians have always done! The formalization of identifying such weak concepts and the paths to take is what makes conceptual engineering particularly interesting in its application to mathematics. The intuitive workflow mathematicians establish in high-level proofs is aided by this simple formalization.
Conclusion
To conclude, we developed an ITT-CE framework for conceptually engineering mathematics, given the system of natural deduction to bound the range of possible domain types for a given mathematical term. During this process, we take into account that these deductions must come to a priori with no axiomatic system developing their logical sequences, therefore we must use hypothetical reasoning to exhaust domain possibilities. We then make use of Haslanger 2005’s manifest/operative/target concepts to construct what each concept we are engineering ought to accomplish. The constructive nature of ITT-CE allows for a simple application of open texturedness and we classify ITT-CE as an unsafe space due to the imperfect mappings from manifest to operative concepts. We make use of Maddy’s goals from Category Theory to build a promising ruleset for verifying our target concepts and describe the fundamental issue with ITT via HoTT. Finally, we suggest this issue can be solved following our general framework for conceptually engineering ITT-CE, and provide a case study for how mathematicians conceptually engineer the concept of coercion.
References
Awodey, Steve, A ́ Pelayo, and M A. Warren (Feb. 2013). Voevodsky’s Univalence Axiom in homotopy type theory. URL: https://www.andrew.cmu.edu/user/awodey/preprints/ NoticesAMS.pdf.
Brouwer, L and (2011). Brouwer’s Cambridge Lectures on Intuitionism. Cambridge University Press.
REFERENCES 17 Chalmers, David J (Oct. 2011). “Verbal disputes”. en. In: Philos. Rev. 120.4, pp. 515–566.
Cohen, Cyril et al. (2016). “Cubical Type Theory: a constructive interpretation of the univalence axiom”. In.
Eades, Harley (2012). Type Theory and Applications. URL: https://ncatlab.org/nlab/ files/EadesTypeTheoryAndApplications.pdf.
Esik, Zoltan, ed. (Sept. 2006). Computer science logic. en. 2006th ed. Lecture notes in computer science. Berlin, Germany: Springer.
Goguen, Joseph A (Mar. 1991). “A categorical manifesto”. en. In: Math. Struct. Comput. Sci. 1.1, pp. 49–67.
Harper, Robert (Mar. 2011). The holy trinity. URL: https://existentialtype.wordpress. com/2011/03/27/the-holy-trinity/.
Haslanger, Sally (2005). “What Are We Talking about? The Semantics and Politics of Social Kinds”. In: Hypatia 20.4, pp. 10–26. ISSN: 08875367, 15272001. URL: http://www.jstor. org/stable/3810885 (visited on 05/06/2023).
Isaac, Manuel Gustavo (Sept. 2021). “Which concept of concept for conceptual engineering?” en. In: Erkenntnis.
Isaac, Manuel Gustavo, Steffen Koch, and Ryan Nefdt (Oct. 2022). “Conceptual engineering: A road map to practice”. en. In: Philos. Compass 17.10.
Lambek, J and P J Scott (June 1986). Cambridge studies in advanced mathematics: Introduction to higher-order categorical logic series number 7. en. Cambridge studies in advanced mathematics. Cambridge, England: Cambridge University Press.
Lawvere, F. William (2003). “Foundations and Applications: Axiomatization and Education”. In: The Bulletin of Symbolic Logic 9.2, pp. 213–224. ISSN: 10798986. URL: http://www.jstor.org/stable/3094791 (visited on 05/22/2023).
Negri, Sara and Jan von Plato (July 2008). Structural Proof Theory. Cambridge, England: Cambridge University Press.
Open Problems in HoTT (n.d.). URL: https://ncatlab.org/nlab/show/open+problems+in+homotopy+type+theory.
Root, Michael (2013). “Resisting Reality: Social Construction and Social Critique”. In: Analysis 73.3, pp. 563–568. ISSN: 00032638, 14678284. URL: http://www.jstor.org/stable/24671140 (visited on 05/06/2023).
Soloviev, Sergei and Zhaohui Luo (Dec. 2001). “Coercion completion and conservativity in coercive subtyping”. en. In: Ann. Pure Appl. Logic 113.1-3, pp. 297–322.
Tanswell, Fenner Stanley (Nov. 2018). “Conceptual engineering for mathematical concepts”. en. In: Inquiry (Oslo) 61.8, pp. 881–913.
Taylor, Paul (May 1999). Cambridge studies in advanced mathematics: Practical foundations of mathematics series number 59. en. Cambridge studies in advanced mathematics. Cambridge, England: Cambridge University Press.
It’s important to note that this framework also clarifies Tanswell’s glossing over language dilemma. As Brouwer put it “Formal language accompanies mathematics as a score accompanies a symphony by Bach or an oratorio by Handel.” We are now purely in the conceptual world, languageless.
Because Haslanger’s methodology supports ITT comfortably, we leave the discussion of constructive set theory for future work. In addition, discussions involving definitional set theory, which make use of type-theoretic (and other) primitive concepts to describe set theory are left for a later date. However, it’s important to remark that such work might ameliorate Tanswell’s ZFC-dependent analysis.
Natural should not be conflated with easy. It might still take an incredible amount of technical ability to get to such conclusions, but the matter of fact is that a conclusion can be reached given the premises. The question of whether this problem is always solvable is one of the key aspects of intuitionism, which for the sake of this paper will be taken for granted.
There is one branch of proof theory, reductive proof theory, that focuses on a similar question type theory tackles: what rests on what? Since this branch reduces classical systems to constructive systems, we would rather skip the ameliorative process on a ZFC approach by bridging the analysis with what theorists call reverse mathematics, which could then be bridged with constructive reverse mathematics, leading to our conclusions in the fully constructive domain. Nonetheless, it’s still interesting to note for future work that such analysis is possible!
It would also be possible to take the trilogy as three distinct manifest concepts which are equivalent.
For the sake of brevity we will not go into detail with this latter issue.
Other benefits are function extensionality and shaping the theory for higher inductive types.